Google's AlphaEvolve tightens MAX-4-CUT hardness - the third decimal just moved

Key results

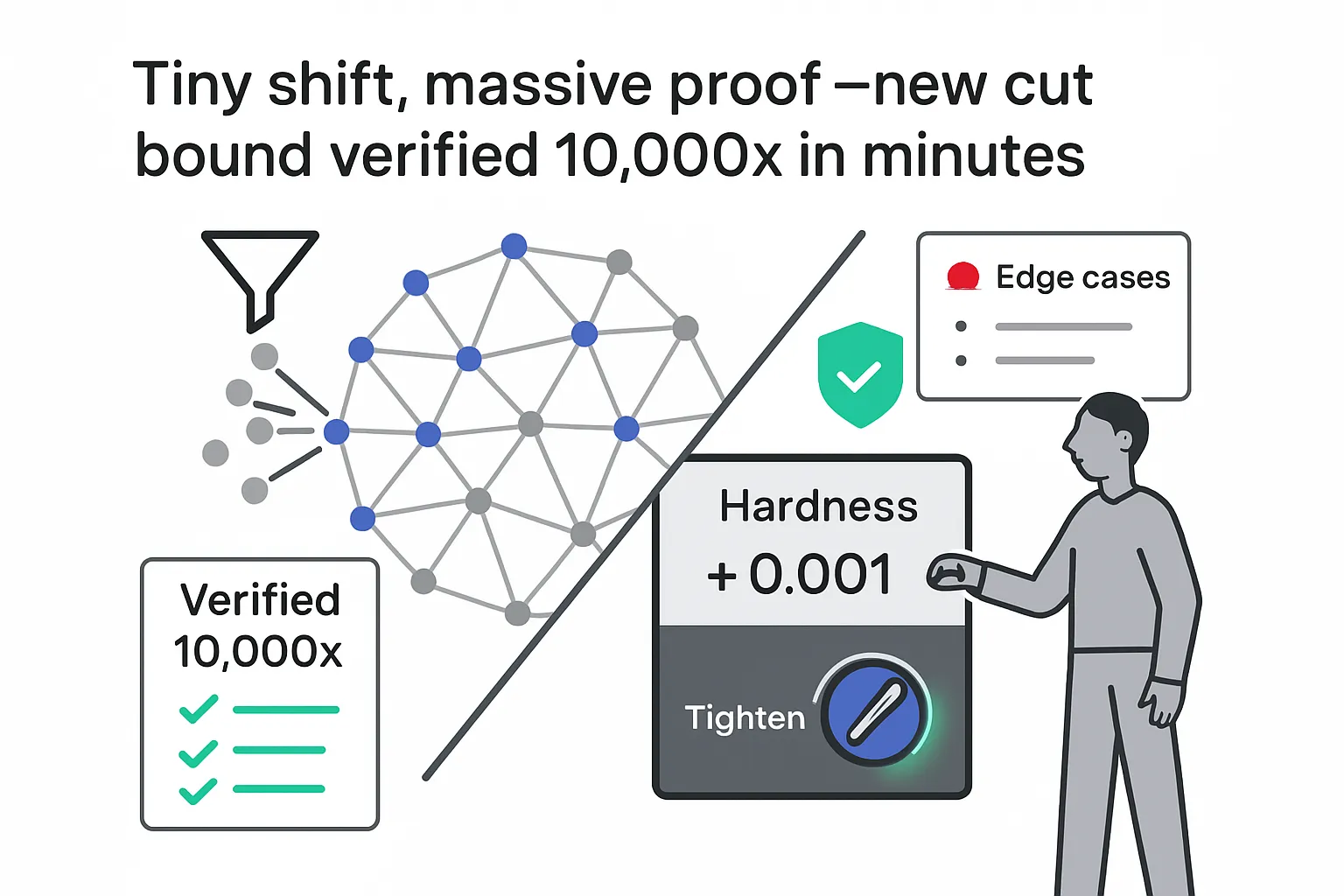
• MAX-4-CUT inapproximability tightened: It is NP-hard to approximate the MAX-4-CUT problem beyond a 0.987 factor, improving the previous 0.9883 bound. The reduction uses a 19-variable gadget with weight ratios up to 1429. MAX-4-CUT asks to partition a graph's nodes into four sets to maximize the sum of weights on edges crossing between sets, a member of the broader maximum cut problem family.
• Average-case certification on random graphs: Guided by AlphaEvolve, the team found Ramanujan graphs with large 2-cuts on instances up to 163 nodes, improving on earlier verifications up to 10 nodes. The associated average-case certification connects to recent work on random graphs.
• Verification at scale: A branch-and-bound based verifier plus system optimizations reportedly delivered roughly a 10,000x speedup, and all final structures were rechecked by brute force.
• Scope: The announcement says these AI-found structures, combined with non-AI algorithmic progress, nearly settle MAX-4-CUT hardness to within the third decimal place.

How AlphaEvolve contributed

AlphaEvolve iteratively evolves code in a feedback loop: it proposes candidate programs, evaluates their outputs against objective functions, selects top performers, and mutates them toward better structures. The resulting combinatorial objects plug into proof frameworks, such as gadget reduction techniques, that lift finite improvements into general theorems in complexity theory.

Background

LLMs have recently demonstrated strong performance in competitive mathematics and competitive programming. In this work, AI assists with constructing hard instances and gadgets that inform limits for efficient approximation algorithms. Hardness-of-approximation results set provable boundaries on what algorithms can achieve, while average-case certification targets properties that hold for typical random instances.

Authors, acknowledgments, and availability

The announcement credits Ansh Nadga, Abhradeep Thakurta, and Prabhakar Raghavan. Acknowledgments include Adam Zsolt Wagner, Swarat Chaudhuri, Pasin Manurangsi, and Sushant Sachdeva.

Read the official announcement, explore the paper, and learn more about AlphaEvolve. The blog post also includes diagrams of the lifting framework, the MAX-4-CUT gadget, and a 4-regular Ramanujan graph.